Gestion de la génération de nombre aléatoire

Note sur la randomisation d'un MCMC

Une première implémentation était basée sur les routines intrasec de génération de nombre aléatoire en fortran :

  • random_number : production de chiffre aléatoire entre 0 et 1
  • random_seed : initialisation du germe de génération

Ce logiciel étant implémenté avec OpenMP ( découpage de l'application en thread ) et qu'il implémente un algorithme monte carlo MCMC (donc fortement liés a la génération de nombre aléatoire)BR, il s'avère qu'il est primordial d'interfacer le logiciel avec une librairie adaptée.

Voici une note de la document du compilateur gfortran (GNU) a propos de la routine random_number :

''«Please note, this RNG is thread safe if used within OpenMP directives, i.e., its state will be consistent while called from multiple threads. However, the KISS generator does not create random numbers in parallel from multiple sources, but in sequence from a single source. If an OpenMP-enabled application heavily relies on random numbers, one should consider employing a dedicated parallel random number generator instead. »''

D'apres la librairie Tina's Random Number Generator Library (TRNG) « le random seeding » n'est pas conseillé : Tous les processus utilise le même PRNG avec un seed different.

On espere ainsi qu'il n y aura pas de recouvrement et que les sous-séquences ne seront pas corrélées. Ceci n'est pas fondé théoriquement, Le random seeding est une violation du conseille de Donald Knuth :

« Les générateurs de nombre ne devraient pas être choisi au hasard ».

Le logiciel GABayes implémente une interface utilisant cette librairies (TRNG) et utilise une stratégie Leapfrog basé sur des pseudo generateur de nombre aléatoire (PRNG), couramment utilisé dans les algorithmes parallèles utilisant la génération de nombre aléatoire.
p. Voici une présentation courte de la librairie, tiré de son site web :

« Tina's Random Number Generator Library (TRNG) is a state of the art C++ pseudo-random number generator library for sequential and parallel Monte Carlo simulations. Its design principles are based on a proposal for an extensible random number generator facility, that will be part of the random number generator facility of the forthcoming revision of the C++ standard. »

Architecture logicielle

Génération de nombre aléatoire pour un MCMC

Il existe 2 implémentations (modules fortran) :
  • Une première implémentation basé sur la routine intrasec fortran random_number
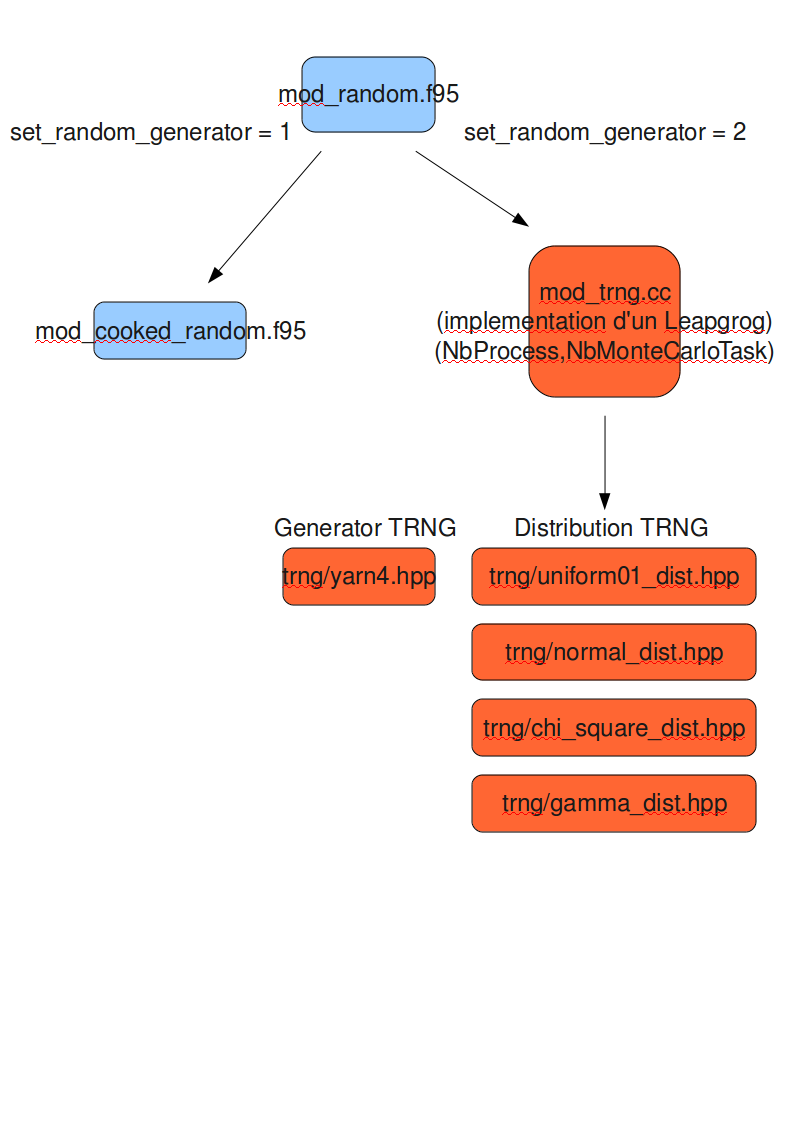
  • Une deuxième implémentation basé sur une librairie utilisant des PRNG (Pseudos Random Number Generator) et adapté au parallelisme OpenMP.

Première stratégie : fonction intrasec fortran

à remplir

Deuxième stratégie : implémentation leapfrog Tina's Random Number Generator Library (TRNG)

Utilisation de la librairie C++ : http://trng.berlios.de/ Tina's Random Number Generator Library (TRNG)

Il est précisé dans la FAQ qu'il n'est pas possible d'appeler les routines de cette librairie en fortran car celle-ci est fortement dépendante du concept objet « template ».
Le logiciel GABayes implémente donc un ensemble de fonction (librairie) développée en c++ et basé sur la méthode leapfrog. Cette librairie est utilisé par le module fortran mod_random du logiciel.

fonction C++ du module C++ mod_trng.cc :
  • extern "C" void init_random_leap(int*nbProc,int *whichProc,int*nbChisq,int*nbNorm,int*nbUnif,int*nbBeta)_
  • extern "C" void release_inside_parallel_random_mode_trng()_
  • extern "C" void trng_normal_leap(int *numRand,float*mean,float*sig,float*res)_
  • extern "C" void trng_random_chisq_leap(int *numRand,int*ndf,float*res)_
  • extern "C" void trng_rand_number_leap(int *numRand,float*res)_
  • extern "C" void trng_random_beta_leap(int *numRand,float*aa,float*bb,float*res)_

Le principe du leapfrog est d'associé un générateur (indépendant) a chacune des taches du MCMC. Cette indépendances recherchée doit être assurée également au niveau des processus parallèles.
Pour créer l'independances entre generateur Tina's RNG propose pour chacun des générateurs définis cette librairie une méthode (fonction au sens C++) ''split''.
On assigne un générateur unique de la facon suivante

  • generateur.split(nb_total_generateurs,id_generateur_courant) : assure l'unicite du générateur courant par rapport a l'ensemble des générateurs instanciés (au total ''nb_total_generateurs'')
  • generateur.split(nb_total_processus,id_processus_courant) : assure l'unicite du générateur du processus courant par rapport au générateur équivalent appartenant à un autre processus.

Un générateur unique est instancié pour chacunes des taches du MCMC :

  • variance residuelle (loi chi2,1 random)
  • moyenne générale (loi normal,1 random)
  • donnees manquantes (loi uniforme, N valeurs manquantes)
  • delta pour chaque SNP (loi uniforme, NMK)
  • effet SNP,beta (loi normal,NMK random<=)
  • pi (loi beta,1 random)

Il y a donc 3 + N + 2*NMK générateurs instancié pour chacun des processus parallèles. 

#include <trng/yarn4.hpp>
#define GENRATOR_TYPE                  trng::yarn4

static GENRATOR_TYPE   *streamsChisq  = NULL;
static GENRATOR_TYPE   *streamsNormal = NULL;
static GENRATOR_TYPE   *streamsUnif   = NULL;
static GENRATOR_TYPE   *streamsBeta   = NULL;

//Directive openMP : les tableaux streamsXXX sont locaux a chaque processus OpenMP
#pragma omp threadprivate (streamsChisq,streamsNormal,streamsUnif,streamsBeta)

Le code suivant illustre le découpage pour assurer l'unicite des générateurs:

 // LEAPFROG Method .
 // allocation of a random number engine for each random we needs
 if ( *nbChisq > 0 ) streamsChisq  = new GENRATOR_TYPE[*nbChisq];
 if ( *nbNorm > 0 ) streamsNormal = new GENRATOR_TYPE[*nbNorm];
 if ( *nbUnif > 0 ) streamsUnif   = new GENRATOR_TYPE[*nbUnif];
 if ( *nbBeta > 0 ) streamsBeta   = new GENRATOR_TYPE[2*(*nbBeta)]; // we used 2 gamma...

 //Number of generator
 int total = *nbChisq + *nbNorm + *nbUnif + 2*(*nbBeta) ;

 //Generator for chi2 random
 for (int j=0;j<*nbChisq;j++) {
        streamsChisq[j].split(total,j);
        streamsChisq[j].split(*nbProc,*whichProc);
 }
 //Generator for normal random
 for (int j=0;j<*nbNorm;j++) {
        streamsNormal[j].split(total,*nbChisq + j);
        streamsNormal[j].split(*nbProc,*whichProc);
    }
 //Generator for uniform random
 for (int j=0;j<*nbUnif;j++) {
        streamsUnif[j].split(total,*nbChisq + *nbNorm + j);
        streamsUnif[j].split(*nbProc,*whichProc);
 }
 //Generator for beta random (using 2 gamma random)
 for (int j=0;j<2*(*nbBeta);j++) {
        streamsBeta[j].split(total,*nbChisq + *nbNorm + *nbUnif + j);
        streamsBeta[j].split(*nbProc,*whichProc);
 }

Chacune de ces fonctions statiques contenue dans le fichier source (mod_trng.cc) est agrémenté des mots clef extern "C" afin d être accessible par le module d'interface (module qui est visible par les autres modules du programme notamment le module de calcul mod_calcul.f95 qui implémente le baésien) mod_random.f95. 
 ! ** TRNG Implementation **
    ! Interface with C++ develppement of mod_trng.cc
    interface
            subroutine release_inside_parallel_random_mode_trng_
            end subroutine release_inside_parallel_random_mode_trng_

            subroutine init_random_leap(nbProc,whichProc,nb_chisq,nb_norm,nb_unif,nb_beta)
                integer ,intent(in) :: nbProc ! number of processor
                integer ,intent(in) :: whichProc  ! numero du processus OpenMP
                integer ,intent(in) :: nb_chisq,nb_norm,nb_unif,nb_beta  ! nombre de generateur
            end subroutine init_random_leap

            subroutine set_block_stream(numRand,blockSize)
                integer ,intent(in) :: numRand  ! nombre de generateur
                integer ,intent(in) :: blockSize ! taille du block
            end subroutine set_block_stream

            subroutine trng_normal_leap(numRand,mean,sig,res)
                 integer ,intent(in) :: numRand    ! index du random
                 real    ,intent(in) :: mean
                 real    ,intent(in) :: sig
                 real    ,intent(out) :: res
            end subroutine trng_normal_leap

            subroutine trng_random_beta_leap(numRand,aa,bb,res)
                 integer ,intent(in) :: numRand    ! index du random
                 real    ,intent(in) :: aa
                 real    ,intent(in) :: bb
                 real    ,intent(out) :: res
            end subroutine trng_random_beta_leap

            subroutine trng_random_chisq_leap(numRand,ndf,res)
                 integer ,intent(in) :: numRand    ! index du random
                 integer ,intent(in) :: ndf
                 real   ,intent(out) :: res
            end subroutine trng_random_chisq_leap

            subroutine trng_rand_number_leap(numRand,res)
                 integer ,intent(in) :: numRand    ! index du random
                 real    ,intent(out) :: res
            end subroutine trng_rand_number_leap
    end interface

Dépendances entre les sources fortran et C++

Liens / Ressources

leap_frog_draw.png (102,72 ko) Olivier Filangi, 02/08/2011 13:10